Ch1 Misc Ex1 Q8 A woman stands on the bank of a frozen lake …

The Problem:

A woman stands on the bank of a frozen lake with a dog by her side. She skims a bone across the ice at a speed of 3 m s1. The bone slows down with deceleration 0.4 m s2, and the dog chases it with acceleration 0.6 ms2. How far out from the bank does the dog catch up with the bone?

A woman stands on the bank of a frozen lake with a dog by her side. She skims a bone across the ice at a speed of 3 m s1.

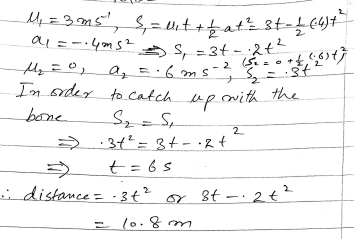
To determine how far from the bank the dog catches up with the bone, we’ll analyze the motion of both the bone and the dog separately and then find the point where their positions are equal.

Given:

• Initial speed of the bone (u_b): 3 m/s
• Deceleration of the bone (a_b): -0.4 m/s² (negative because it’s slowing down)
• Acceleration of the dog (a_d): 0.6 m/s²
• Initial speed of the dog (u_d): 0 m/s (assuming the dog starts from rest)

Objective:

Find the distance from the bank where the dog catches up with the bone.

Step 1: Determine the time when the dog catches the bone

We’ll use the equations of motion to find the time t at which both the bone and the dog have traveled the same distance.

For the bone:

The bone is decelerating, so its speed decreases over time. The distance traveled by the bone as a function of time is:

sb(t) = ub * t + (1/2) * ab * t2

Plugging in the known values:

sb(t) = 3t - 0.2t2

For the dog:

The dog starts from rest and accelerates. The distance traveled by the dog as a function of time is:

sd(t) = ud * t + (1/2) * ad * t2

Plugging in the known values:

sd(t) = 0.3t2

Step 2: Set the distances equal to find the time

To find when the dog catches the bone, set s_b(t) = s_d(t):

3t - 0.2t2 = 0.3t2

Step 3: Solve for t

Combine like terms:

3t = 0.3t2 + 0.2t2

3t = 0.5t2

Rearrange the equation:

0.5t2 - 3t = 0

Factor out t:

t(0.5t - 3) = 0

This gives two solutions:

1. t = 0 (which is the initial time when both are at the bank)
2. 0.5t – 3 = 0 → 0.5t = 3 → t = 6 seconds

So, the dog catches the bone after 6 seconds.

Step 4: Calculate the distance from the bank

Now, we’ll find the distance traveled by either the bone or the dog in 6 seconds. Let’s use the dog’s distance equation for simplicity:

sd(t) = 0.3t2

Plugging in t = 6:

sd(6) = 0.3 * (6)2 = 0.3 * 36 = 10.8 meters

Conclusion

The dog catches up with the bone 10.8 meters from the bank of the frozen lake.