Ch1 Misc Ex1 Q3 A cyclist, travelling with constant acceleration along a straight road …

The Problem

A cyclist, travelling with constant acceleration along a straight road, passes three points A, B and C, where AB = BC= 20 m. The speed of the cyclist at A is 8 ms and at B is 12 m s. Find the speed of the cyclist at C. (OCR)

---

Douglas Quadling Mechanics1 Miscellaneous Exercise1 Q3

A cyclist, travelling with constant acceleration along a straight road, passes three points A, B and C, where AB = BC= 20 m.

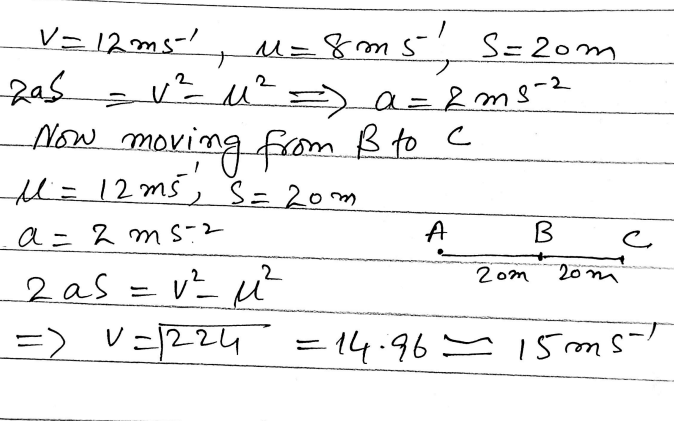
Finding the Speed of a Cyclist at Point C

Introduction

In this problem, we analyze the motion of a cyclist who is moving with a constant acceleration along a straight road. The cyclist passes through three points: A, B, and C, with equal distances between them. Using kinematic equations, we will determine the speed of the cyclist at point C.

Given Data:

• Initial speed at A, u_A = 8 m/s
• Speed at B, v_B = 12 m/s
• Distance between A and B, AB = 20 m
• Distance between B and C, BC = 20 m
• Acceleration, a (unknown, to be determined)
• Final speed at C, v_C (to be determined)

Step 1: Find the Acceleration

To find the acceleration, we use the kinematic equation:

v² = u² + 2as

Applying this equation for motion from A to B:

(12)² = (8)² + 2a(20)

144 = 64 + 40a

40a = 80

a = 2 m/s²

Step 2: Find the Speed at C

Now, applying the same equation for motion from B to C:

vC² = vB² + 2as

vC² = (12)² + 2(2)(20)

vC² = 144 + 80

vC² = 224

vC = √224 ≈ 14.97 m/s

Final Answer:

• Acceleration = 2 m/s²
• Speed at C = 14.97 m/s

Detailed Explanation

Understanding the problem requires knowledge of motion with uniform acceleration. The equations of motion are derived from calculus and describe how velocity, acceleration, and displacement are interrelated.

1. Understanding Acceleration

Acceleration is the rate of change of velocity. In this case, the cyclist’s velocity is increasing uniformly, which means a constant force is acting in the forward direction. The acceleration can be found using:

a = (v² - u²) / (2s)

This equation eliminates time and directly relates velocity, acceleration, and displacement.

2. Applying the Equation to Find Speed at C

Since the acceleration remains constant, we use the same equation for motion from B to C, ensuring we get a smooth transition in velocity.

Concept Check: Why Use This Equation?

We use v² = u² + 2as instead of other kinematic equations because:

• We do not have time as a given variable.
• The equation directly connects velocity, displacement, and acceleration.
• It simplifies calculations without requiring additional steps.

Additional Real-World Applications

This concept is useful in various real-life scenarios such as:

• Analyzing the speed of a car moving along a highway with constant acceleration.
• Determining the landing speed of an aircraft on a runway.
• Predicting the motion of objects in physics experiments.

Conclusion

By applying kinematic equations, we successfully determined the acceleration and the final speed of the cyclist at C. The acceleration was found to be 2 m/s², and the speed at C was calculated as 14.97 m/s.

Key Takeaways

• Use the equation v² = u² + 2as when time is unknown.
• Constant acceleration simplifies motion analysis.
• Understanding motion equations helps in solving real-world problems in mechanics.

Hopefully, this detailed breakdown clarifies the concepts and steps used in solving such problems. Stay tuned for more physics solutions!