The problem:
A train travels from a station P to the next station Q, arriving at Q exactly 5 minutes after leaving P. The (t,v) graph for the train’s journey is approximated by three straight line segments, as shown in the figure. (i) Write down the acceleration of the train during the first minute of the journey. (ii) Find the distance from P to Q.
A train travels from a station P to the next station Q, arriving at Q exactly 5 minutes after leaving P…………..
Douglas Quadling Mechanics1 Miscellaneous Exercise1 Q10(a)& Q10(b)
A train travels from a station P to the next station Q, arriving at Q exactly 5 minutes after leaving P……
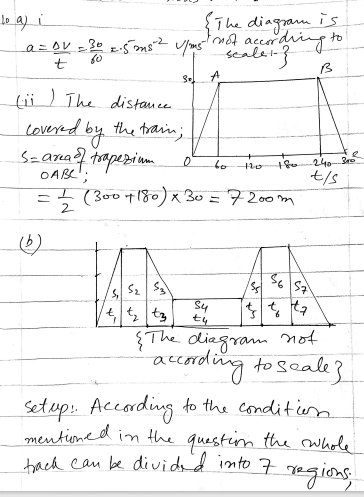
Douglas Quadling Mechanics1 Miscellaneous Exercise1 Q10(b)&Q10(c)
A train travels from a station P to the next station Q, arriving at Q exactly 5 minutes after leaving P…….


A train travels from a station P to the next station Q, arriving at Q exactly 5 minutes after leaving P……
Solution:
(i) Acceleration during the First Minute (0 to 60 seconds):
Acceleration = (Final Velocity – Initial Velocity) / Time
Given: Initial Velocity = 0 m/s, Final Velocity = 30 m/s, Time = 60 seconds
Acceleration = (30 – 0) / 60 = 0.5 m/s²
Answer: Acceleration = 0.5 m/s²
(ii) Distance from P to Q:
The total distance is the sum of distances covered in each segment:
1. First Segment (0 to 60 seconds):
Distance = Initial Velocity * Time + 0.5 * Acceleration * Time²
Given: Initial Velocity = 0 m/s, Acceleration = 0.5 m/s², Time = 60 seconds
Distance = 0 * 60 + 0.5 * 0.5 * (60)² = 900 meters
2. Second Segment (60 to 240 seconds):
Distance = Velocity * Time
Given: Velocity = 30 m/s, Time = 180 seconds
Distance = 30 * 180 = 5400 meters
3. Third Segment (240 to 300 seconds):
Distance = Initial Velocity * Time + 0.5 * Acceleration * Time²
Given: Initial Velocity = 30 m/s, Final Velocity = 0 m/s, Time = 60 seconds
Acceleration = (0 – 30) / 60 = -0.5 m/s²
Distance = 30 * 60 + 0.5 * (-0.5) * (60)² = 900 meters
Total Distance:
Total Distance = 900 + 5400 + 900 = 7200 meters
Answer: Total Distance = 7200 meters
(b) Solution:
Step 1: Break the Journey into Segments
The journey is divided into 7 segments:
- Acceleration Phase: From 0 to 30 m/s.
- Travel at 30 m/s: Before decelerating to 10 m/s.
- Deceleration Phase: From 30 m/s to 10 m/s.
- Restricted Section: Travel at 10 m/s for 2000 meters.
- Acceleration Phase: From 10 m/s to 30 m/s.
- Travel at 30 m/s: After exiting the restricted section.
- Deceleration Phase: From 30 m/s to 0.
Step 2: Calculate Time and Distance for Each Segment
1. Acceleration Phase (0 to 30 m/s):
Acceleration = 0.5 m/s²
Time taken = 60 seconds
Distance covered = 900 meters
2. Travel at 30 m/s (Before Decelerating to 10 m/s):
Distance traveled = 900 meters
Time taken = 30 seconds
3. Deceleration Phase (30 m/s to 10 m/s):
Deceleration = -0.5 m/s²
Time taken = 40 seconds
Distance covered = 800 meters
4. Restricted Section (2000 meters at 10 m/s):
Time taken = 200 seconds
5. Acceleration Phase (10 m/s to 30 m/s):
Acceleration = 0.5 m/s²
Time taken = 40 seconds
Distance covered = 800 meters
6. Travel at 30 m/s (After Exiting Restricted Section):
Distance traveled = 900 meters
Time taken = 30 seconds
7. Deceleration Phase (30 m/s to 0):
Deceleration = -0.5 m/s²
Time taken = 60 seconds
Distance covered = 900 meters
Step 3: Total Time
Total Time = 60 + 30 + 40 + 200 + 40 + 30 + 60 = 460 seconds
Final Answer:
The train takes 460 seconds to travel from P to Q on this occasion.
(c)
Solution:
Part 1: Prove the Distance Traveled is 2V² – 100:
The journey consists of two phases:
- Acceleration Phase: From rest (0 m/s) to V m/s.
- Deceleration Phase: From V m/s to 10 m/s.
1. Acceleration Phase:
Acceleration = 0.5 m/s²
Time taken = 2V seconds
Distance covered = V² meters
2. Deceleration Phase:
Deceleration = -0.5 m/s²
Time taken = 2(V – 10) seconds
Distance covered = V² – 100 meters
Total Distance:
Total Distance = V² + (V² – 100) = 2V² – 100 meters
Part 2: Determine if the Train Could Make Up Lost Time:
From part (b), the train takes 460 seconds with the speed restriction. Without the restriction, it would take 300 seconds. The time lost due to the restriction is 160 seconds.
To make up the lost time, the train would need to travel faster than 30 m/s. However, the fixed acceleration and deceleration rates prevent this. Thus, the train cannot make up the lost time.
Final Answer:
1. The distance traveled is 2V² – 100.
2. The train cannot make up the lost time by exceeding the normal speed of 30 m/s.
