The Problem:
A car starts from rest at the point A and moves in a straight line with constant acceleration for 20 seconds until it reaches the point B. The speed of the car at B is 30 m s. Calculate (a) the acceleration of the car, (b) the speed of the car as it passes the point C, where C is between A and B and AC = 40 m. (OCR)
Understanding Car Acceleration – A Real-Life Approach
Introduction
Acceleration is something we experience in everyday life, whether we realize it or not. When we press the gas pedal in a car, we feel a push back into our seat. When a roller coaster takes off, we experience a sudden force . Even when we start running, our body goes from a resting position to moving faster and faster.
But how do we measure acceleration? How can we calculate how fast an object, like a car, picks up speed over time?
In this post, we will break down a classic mechanics problem from Douglas Quadling’s A-Level Mechanics. We will solve it using two different methods—first, by applying the equations of motion, and second, by using energy principles. Both methods will lead us to the same answer, proving that physics has multiple ways of looking at a problem.
HandWritten Solution:
Douglas Quadling Mechanics1 Miscellaneous Exercise1 Q1
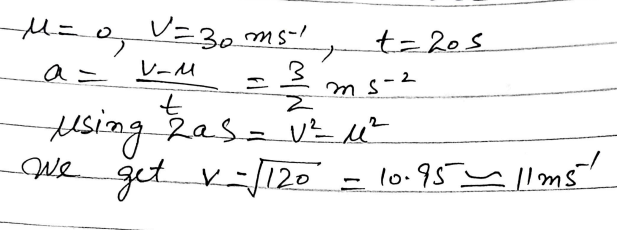
The Scenario – A Car Picking Up Speed
Imagine a car that starts from rest at a point A and moves in a straight line with constant acceleration. After 20 seconds, it reaches a point B, where its speed is 30 m/s.
Our goals are to:
- Find the acceleration of the car.
- Determine the speed at another point, C, which is 40 meters away from A.
To solve this, let’s break the problem down step by step.
Solution 1: Using the Equations of Motion
The equations of motion are a set of formulas that describe the relationship between velocity, acceleration, time, and displacement. These are especially useful when acceleration is constant, as in this case.
Step 1: Finding Acceleration
The first equation we use is:
v = u + at
where:
- u = 0 (since the car starts from rest)
- v = 30 m/s (final speed at B)
- t = 20 seconds
- a is what we need to find
Substituting the values:
30 = 0 + (a × 20)
a = 30 ÷ 20 = 1.5 m/s²
So, the acceleration of the car is 1.5 m/s².
This means that for every second that passes, the car gains 1.5 meters per second in speed. If you were driving this car, you’d feel a steady, smooth push forward as the car speeds up.
Step 2: Finding the Speed at Point C
Next, we determine the speed of the car when it reaches point C, which is 40 meters from A.
We use another kinematic equation:
v² = u² + 2as
where:
- u = 0 (initial speed)
- a = 1.5 m/s² (from previous step)
- s = 40 m (distance to C)
Now, substituting the values:
v² = 0 + (2 × 1.5 × 40)
v² = 120
v = √120 ≈ 10.95 m/s
Rounded to two significant figures, the speed at point C is 11 m/s.
So, by the time the car has traveled 40 meters, it has already gained a significant amount of speed!
Solution 2: Using the Energy Approach
Last week, i visited a factory in Hattar Industrial Area and discussed this method for safe braking system and they appreciated me
Another way to solve this problem is by using the principle of work and energy.
This principle states that the change in kinetic energy of an object is equal to the work done by force. In simpler terms, energy is transferred into the car as it speeds up.
The formula for kinetic energy is:
(1/2) m v² – (1/2) m u² = F × s
Since force F = ma, we rewrite this as:
(1/2) v² – (1/2) u² = a × s
Step 1: Finding Acceleration
Applying the equation for point B (s = 300 m, v = 30 m/s, u = 0):
(1/2) × (30)² – (1/2) × (0)² = a × 300
450 = 300a
a = 450 ÷ 300 = 1.5 m/s²
This confirms our previous answer.
Step 2: Finding Speed at Point C
Now, using the equation at C (s = 40 m):
(1/2) v² – (1/2) × (0)² = 1.5 × 40
(1/2) v² = 60
v² = 120
v = √120 ≈ 11 m/s
Once again, we get 11 m/s at point C, confirming our previous result.
How This Relates to Real Life
🚗 Driving & Braking
- Knowing how acceleration works helps drivers estimate how long it takes to reach a specific speed.
- Engineers use these equations to design safe braking systems in cars.
🏃♂️ Sports & Athletics
- Sprinters, cyclists, and swimmers accelerate at the start of a race using similar principles.
- Understanding acceleration helps coaches design better training programs for athletes.
🚀 Space & Engineering
- Rockets experience changing acceleration during launch.
- Scientists use motion equations to calculate escape velocity and fuel efficiency.
Conclusion
We solved this problem in two different ways:
- Using kinematics equations (equations of motion).
- Using the work-energy principle.
Both methods gave us the same results:
- The car’s acceleration is 1.5 m/s².
- The speed at point C is 11 m/s.
These concepts aren’t just for textbooks! Understanding acceleration helps us in driving, sports, engineering, and even space exploration.
