The Problem:
A train goes into a tunnel at 20 m/s and emerges from it at 55 m/s. The tunnel is 1500 m long. Assuming constant acceleration, find how long the train is in the tunnel for, and the acceleration of the train.
Douglas Quadling Mechanics1 Exercise1C Q2
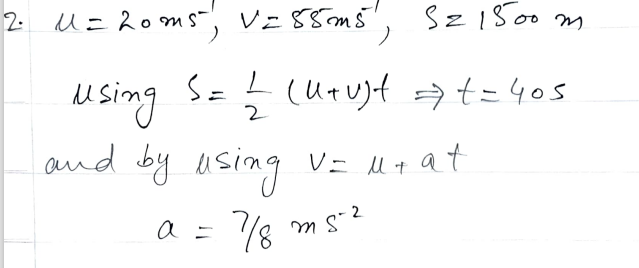
Problem: A train enters a tunnel at 20 m/s and emerges at 55 m/s. The tunnel is 1500 meters long. Assuming constant acceleration, find:
- How long the train is in the tunnel.
- The acceleration of the train.
Solution:
Step 1: Understand the Problem
We are given:
- Initial speed (u) = 20 m/s (speed at entry).
- Final speed (v) = 55 m/s (speed at exit).
- Distance (s) = 1500 meters (length of the tunnel).
- Acceleration (a) = constant (unknown).
- Time (t) = unknown (time spent in the tunnel).
We need to find:
- The time (t) the train is in the tunnel.
- The acceleration (a) of the train.
Step 2: Use the Equations of Motion
Since the train has constant acceleration, we use the equations of motion:
- v = u + at (relates speed, acceleration, and time).
- v² = u² + 2as (relates speed, acceleration, and distance).
Step 3: Solve for Acceleration (a)
Use the equation v² = u² + 2as to find a.
Substitute the known values:
- v = 55 m/s,
- u = 20 m/s,
- s = 1500 m.
Equation:
55² = 20² + 2 * a * 1500
3025 = 400 + 3000a
Subtract 400 from both sides:
3025 – 400 = 3000a
2625 = 3000a
Divide both sides by 3000:
a = 2625 / 3000
a = 0.875 m/s²
So, the acceleration of the train is 0.875 m/s².
Step 4: Solve for Time (t)
Use the equation v = u + at to find t.
Substitute the known values:
- v = 55 m/s,
- u = 20 m/s,
- a = 0.875 m/s².
Equation:
55 = 20 + 0.875t
Subtract 20 from both sides:
55 – 20 = 0.875t
35 = 0.875t
Divide both sides by 0.875:
t = 35 / 0.875
t = 40 seconds
So, the train is in the tunnel for 40 seconds.
Final Answers:
- The train is in the tunnel for 40 seconds.
- The acceleration of the train is 0.875 m/s².
Summary:
- Time in tunnel (t): 40 seconds.
- Acceleration (a): 0.875 m/s².
