The Problem:
A downhill skier crosses the finishing line at a speed of 30 m/s and immediately starts to decelerate at 10 m/s. There is a barrier 50 metres beyond the finishinyg line. (a) Find an expression for the skier’s speed when she is s metres beyond the finishing line. (b) How fast is she travelling when she is 40 metres beyond the finishing line? (c) How far short of the barrier does she come to a stop? (d) Display an (s, v) graph to illustrate the motion.
Douglas Quadling Mechanics1 Exercise1C Q7
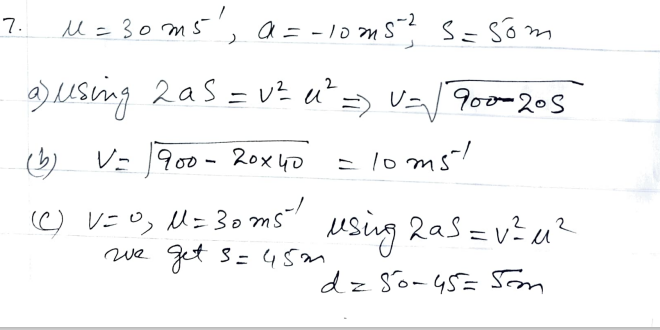
Solution
Given Data:
- Initial speed, u = 30 m/s
- Deceleration, a = -10 m/s²
- Distance beyond the finish line, s
(a) Expression for the skier’s speed when she is s meters beyond the finishing line:
Using the kinematic equation:
v² = u² + 2as
Substituting values:
v² = 30² + 2(-10)s
v² = 900 – 20s
Taking the square root:
v = sqrt(900 – 20s)
(b) Speed when she is 40 meters beyond the finishing line:
Substituting s = 40:
v = sqrt(900 – 20(40))
v = sqrt(900 – 800)
v = sqrt(100) = 10 m/s
(c) Distance short of the barrier where she stops:
The skier stops when v = 0, so:
0 = 900 – 20s
s = 900 / 20 = 45 meters
Since the barrier is 50 meters away, she stops:
50 – 45 = 5 meters short of the barrier.
