The Problem:
An ocean liner leaves the harbour entrance travelling at 3 m s1, and accelerates at 0.04 m s2 until it reaches its cruising speed of 15 m s1. (a) How far does it travel in accelerating to its cruising speed? (b) How long does it take to travel 2 km from the harbour entrance?
Douglas Quadling Mechanics1 Exercise1C Q6
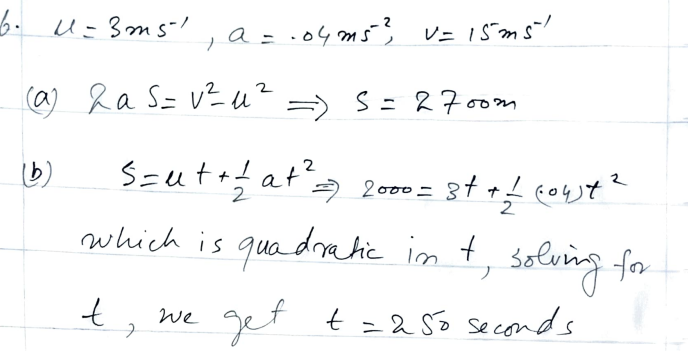
Problem: An ocean liner leaves the harbour entrance traveling at 3 m/s and accelerates at 0.04 m/s² until it reaches its cruising speed of 15 m/s. Find:
- How far it travels while accelerating to its cruising speed.
- How long it takes to travel 2 km from the harbour entrance.
Solution:
Step 1: Understand the Problem
We are given:
- Initial speed (u) = 3 m/s.
- Acceleration (a) = 0.04 m/s².
- Final speed (v) = 15 m/s (cruising speed).
- Distance (s) = unknown (for part a).
- Time (t) = unknown (for part b).
We need to find:
- The distance traveled while accelerating to cruising speed.
- The time taken to travel 2 km (2000 meters) from the harbour entrance.
Step 2: Solve for Distance Traveled While Accelerating
We use the equation of motion:
v² = u² + 2as
Substitute the known values:
- v = 15 m/s,
- u = 3 m/s,
- a = 0.04 m/s².
Equation:
15² = 3² + 2 * 0.04 * s
225 = 9 + 0.08s
Subtract 9 from both sides:
225 – 9 = 0.08s
216 = 0.08s
Divide both sides by 0.08:
s = 216 / 0.08
s = 2700 meters
So, the ocean liner travels 2700 meters while accelerating to its cruising speed.
Step 3: Solve for Time to Travel 2 km
We need to find the time taken to travel 2 km (2000 meters) from the harbour entrance.
Step 3.1: Check if the Ocean Liner Reaches Cruising Speed Within 2 km
From part (a), we know the ocean liner takes 2700 meters to reach cruising speed. Since 2000 meters is less than 2700 meters, the ocean liner is still accelerating during this time.
Step 3.2: Use the Equation of Motion
We use the equation:
s = ut + (1/2)at²
Substitute the known values:
- s = 2000 meters,
- u = 3 m/s,
- a = 0.04 m/s².
Equation:
2000 = 3t + (1/2) * 0.04 * t²
Simplify:
2000 = 3t + 0.02t²
Rearrange into a quadratic equation:
0.02t² + 3t – 2000 = 0
Multiply through by 100 to eliminate decimals:
2t² + 300t – 200000 = 0
Divide through by 2:
t² + 150t – 100000 = 0
Step 3.3: Solve the Quadratic Equation
Use the quadratic formula:
t = [-b ± √(b² – 4ac)] / (2a)
Where:
- a = 1,
- b = 150,
- c = -100000.
Substitute the values:
t = [-150 ± √(150² – 4 * 1 * (-100000))] / (2 * 1)
t = [-150 ± √(22500 + 400000)] / 2
t = [-150 ± √422500] / 2
t = [-150 ± 650] / 2
We discard the negative root since time cannot be negative:
t = (-150 + 650) / 2
t = 500 / 2
t = 250 seconds
So, the ocean liner takes 250 seconds to travel 2 km from the harbour entrance.
Final Answers:
- The ocean liner travels 2700 meters while accelerating to its cruising speed.
- It takes 250 seconds to travel 2 km from the harbour entrance.
Summary:
- Distance traveled while accelerating: 2700 meters.
- Time to travel 2 km: 250 seconds.
