The Problem:
A train is travelling at 80 m/s when the driver applies the brakes, producing a deceleration of 2 m/s^2 for 30 seconds. How fast is the train then travelling, and how far does it travel while the brakes are on?
Douglas Quadling Mechanics 1
Exercise 1B Q6
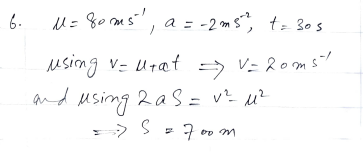
Step 1: Find the final speed of the train
We are given:
- Initial velocity, u = 80 m/s,
- Deceleration, a = -2 m/s² (negative because it’s slowing down),
- Time, t = 30 seconds.
We use the equation:
v = u + at
Substitute the known values:
v = 80 + (-2)(30)
v = 80 – 60
v = 20 m/s
Step 2: Find the distance traveled during braking
We use the equation:
s = ut + 0.5at²
Substitute the known values:
s = 80(30) + 0.5(-2)(30²)
s = 2400 + 0.5(-2)(900)
s = 2400 – 900
s = 1500 m
Final Answers:
- The train’s final speed after braking: v = 20 m/s,
- The distance traveled while braking: s = 1500 m.
